Estimación de Distancias Inaccesibles

La estimación de distancias inaccesibles es una labor importantísima para un explorador, por ejemplo para realizar un croquis, cuando dibujamos un río en un mapa y quisiéramos indicar su ancho con una precisión mayor que la simple estimación "al ojo" (aunque un verdadero explorador debería tener la posibilidad de hacer mediciones muy exactas "al ojo").

También podemos necesitar medir el ancho para calcular el largo de los troncos y sogas necesarios para elaborarlo. Seria una lástima equivocarnos al medir "al ojo" el ancho, sea que nos falte material o que hayamos derribado más árboles de lo necesario.

Todo esto se evita con un método de medición seguro. Cuando elaboramos el mapa y debemos representar un camino es relativamente fácil pues el largo y el ancho se determinan fácilmente contando una serie de pasos. No ocurre esto con un río. Si el río es turbulento o profundo no podríamos pasar simplemente caminando por encima. Entonces buscamos una forma de "trasladar" la medida del río a tierra firme, en dónde podemos tranquilamente contar los pasos. Esta es la finalidad de los dos sistemas de estimación que describiremos.

SOMBRERO

Es el método más sencillo, aunque tiene la desventaja de su poca exactitud, la cual depende de la pericia del que realiza la medición. La idea es representar un "compás óptico" de la siguiente manera:

1. La persona que hará la medición debe tener puesto un sombrero o visera con el a la rígida. En el caso del sombrero tipo safari (de uniforme) se abrochan los lados para que el extremo delantero mantenga una forma rígida.

2. Debe estar ubicado en un terreno plano, sin baches y totalmente horizontal (sin cuestas de subida o de bajada)

3. Se para uno en la orilla del río, poniendo una marca en éste lugar.

4. Sin moverse de la marca, se mira a la orilla opuesta y se sube o baja la frente de modo que hagamos coincidir en forma visual el borde de la orilla opuesta con el borde del ala del sombrero.

5. Sin subir ni bajar la cabeza ni moverse del lugar dónde se encuentra, se debe girar hacia tierra firme, mirando en dónde es que coincide la línea del ala del sombrero con la tierra, buscando un punto que nos sirva de referencia, tal como una piedra, o mejor aún,  es que otra persona se pare en el lugar de esta coincidencia , lo cual le indicaremos nosotros.

6. Ahora podemos proceder a "talonear" (medir los pasos) desde donde nos encontramos (que hemos dejado marcado) hasta la nueva marca que hemos hecho.

Esta distancia corresponde aproximadamente a la distancia desde dónde se tomó la medida (primera marca) hasta la orilla opuesta.

Como hemos dicho este método no es tan exacto, ya que tiene dos puntos de posible error: el momento de girar la cabeza, que se puede mover sensiblemente hacia arriba o hacia abajo, y la toma de los pasos de una marca hacia otra.

Una forma de remediar en algo esta situación es repetir el proceso, no una , sino tres veces, obteniendo luego un promedio aritmético, así:

(1raMedida + 2daMedida +3raMedida)/3 = MedidaAproximada

 

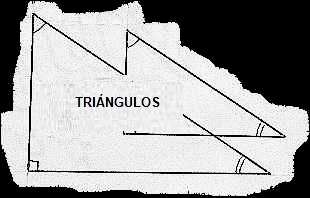
TRIÁNGULOS

Mucho más exacto que el anterior, bien aplicado no debe tener un error sensible en la apreciación de distancia.

Se basa en una aplicación práctica de la trigonometría, rama de las matemáticas que estudia los triángulos, específicamente la "ley de proporcionalidad de triángulos rectángulos". Muchos de los instrumentos de medición se basan en estas leyes (Sextantes, Eclímetros, Teodolitos, etc.).

El método en sí requiere del uso de un mínimo de cuatro rocas o estacas que serán usadas como marcas. Procederemos según los siguientes pasos:

1. Al igual que en el método de Sombrero, se busca una zona horizontal en la orilla en que estamos que no tenga baches, ni cuestas, que sea horizontal (sin subidas ni bajadas)

2. Se busca un "Punto de Referencia" en la orilla opuesta. Tal como una roca, un árbol u otro que sea fácilmente reconocible y que esté lo más próximo posible al río.

3. Coloca una de las marcas exactamente al frente de el punto de referencia, en la orilla en que estás parado. A esta la llamaremos "Marca A"

4. Camina 20 (o 40 pasos)  en forma paralela a la orilla del río (perpendicularmente a la dirección del punto de referencia y a la marca A, es decir, haciendo una "L") y pon la segunda marca, esta será la "Marca B"

5. Ahora sigue caminando en la misma dirección de las marcas "A" y "B", pero esta vez una distancia igual a la mitad de la distancia de A hacia B, por ejemplo, si caminaste  ya 20 pasos, ahora camina 10 (Si la distancia era de 40 pasos, camina ahora 20 pasos mas) Aquí pon la tercera marca, la "Marca C"

6. Ahora camina tierra adentro, haciendo otro giro perpendicular, hasta que veas que el "Punto de Referencia" en la orilla opuesta y la "Marca B" estén en la misma línea. Este punto lo llamaremos "Marca D"

7. La Distancia de la "Marca C" a la "Marca D" es igual a la mitad de la distancia de la "Marca A" al "Punto de Referencia" elegido en la orilla opuesta. Es decir, finalmente para tener la distancia del río debes medir la distancia de la "Marca C" a la "Marca D" y duplicarla. Como ya dijimos, si es bien aplicado el margen de error resulta muy pequeño.

TRIÁNGULACIÓN CON BRÚJULA

Mucho más exacto y mas fácil aún, eso si requier del dominio del uso de la brújula y de el uso de una hoja auxiliar. En realidad lo que harás será haer un croquis de la distancia usando la brújula y luego la medirás convirtiendo la medida usando la respectiva escala. Para mas detalles ver: Croquis y Plancheta  

De la sección de "Croquis" extraémos el siguiente pàrrafo:

"...marca el punto en el mapa donde te encuentras y mide la dirección en grados hasta la cumbre (y la señalas en el papel) y luego continúa caminando. Un tramo más allá vuelve a tomar la medida (marcando el punto en el papel) y vuelve a tomar la lectura a la cumbre, la cual debe haber cambiado sensiblemente. Marca la nueva lectura en el papel y verás que las líneas de las lecturas a la cumbre se cruzan en un punto. Este es el punto exacto dónde se encuentra la cumbre y la proporción queda marcada en escala. Todo este procedimiento se llama TRIANGULACIÓN. Con este método puedes determinar una serie de distancias y puntos del mapa, más lejanos (de hecho, es en este método en que se basa la "Plancheta").